En algèbre linéaire, maîtriser la construction de la matrice d’une application linéaire est crucial !
C’est ce qui fait la différence entre réussir brillamment ou se perdre dans ses examens 😫
C’est bien plus qu’une simple technique; c’est une compétence essentielle qui, une fois acquise, te fera gagner du temps et te distinguera des autres lors de tes concours ✨
Tu pourrais penser que c’est complexe, mais détrompe-toi !
Cette méthode est bien plus accessible qu’il n’y paraît 😉
En suivant des étapes claires et structurées, tu transformeras non seulement ta compréhension des applications linéaires mais aussi ta manière de les étudier !
Avec la technique que je vais te dévoiler, les erreurs dans la construction des matrices seront de l’histoire ancienne, indépendamment de la façon dont l’application linéaire est présentée 😎
Imagine, ne plus jamais douter lors de la création d’une matrice, te garantissant ainsi de briller en algèbre linéaire lors de tes prochaines examens 💪
1️⃣ On pose le problème
Afin de faire la matrice d’une application linéaire, on a besoin de plusieurs ingrédients :
- D’un espace vectoriel de départ E de dimension finie p
- D’un espace vectoriel d’arrivée F de dimension finie n
- D’une base pour l’espace vectoriel de départ E : $$ \mathit{B}=\left\{ e_{1},\cdots , e_{p}\right\}$$
- D’une base pour l’espace vectoriel d’arrivé F : $$\mathit{B’}=\left\{ \epsilon _{1},\cdots , \epsilon _{n}\right\}$$
- D’une application linéaire reliant les deux espaces vectoriels $$f : E\rightarrow F$$
2️⃣ Calculs d'images
La clé pour la construction d’une matrice d’une application linéaire est le calcul d’images !
C’est pour cela que dans cette partie, nous allons voir comment transformer les éléments de la base d’un espace vectoriel pour créer notre matrice 🤩
C’est ici que toute la magie opère, où chaque vecteur de notre base de départ se voit attribuer une nouvelle expression en fonction des vecteurs de l’espace d’arrivée 🌟
En pratique comment ça se passe ?
Tu vas prendre les éléments de ta base de départ \(\mathit{B}\) et tu vas calculer leur image par l’application linéaire f !
Mais le but n’est pas juste de calculer ces images, il faut surtout les exprimer avec les éléments de ta base d’arrivée \(\mathit{B’}\) afin de créer un lien entre les deux 🎗
$$f(e_{1})=a_{11}\epsilon _{1}+a_{21}\epsilon _{2}+\cdots +a_{n1}\epsilon _{n}$$
$$f(e_{2})=a_{12}\epsilon _{1}+a_{22}\epsilon _{2}+\cdots +a_{n2}\epsilon _{n}$$
$$\vdots$$
$$f(e_{p})=a_{1p}\epsilon _{1}+a_{2p}\epsilon _{2}+\cdots +a_{np}\epsilon _{n}$$
En exprimant les images des éléments de la base de départ en fonction des éléments de la base d’arrivée, tu vas faire apparaître des coefficients \(a_{ij}\)
Et ce sont ces coefficients qui sont la clé de ta construction matricielle !
D’ailleurs ce n’est pas pour rien que je les ai écrit d’une certaine manière 😏
3️⃣ Construction de la matrice
Ça y est, après avoir exploré les bases et calculé les images, nous voici arrivés au moment tant attendu : la construction de la matrice !
Cette étape est le cœur battant de l’algèbre linéaire, où tous les éléments que nous avons préparés prennent forme pour révéler la structure complète de notre application linéaire !
C’est ici que tu vas assembler le puzzle, en plaçant chaque image calculée dans la matrice qui deviendra ton plus fidèle outil pour résoudre des problèmes complexes d’applications linéaires
Comment placer ces images miracles ?
Tu vas tout simplement les placer en colonne dans ta matrice, plus précisément tu vas placer les coefficients de ta première image dans la première colonne, les coefficients de ta deuxième image dans la seconde colonne, etc…
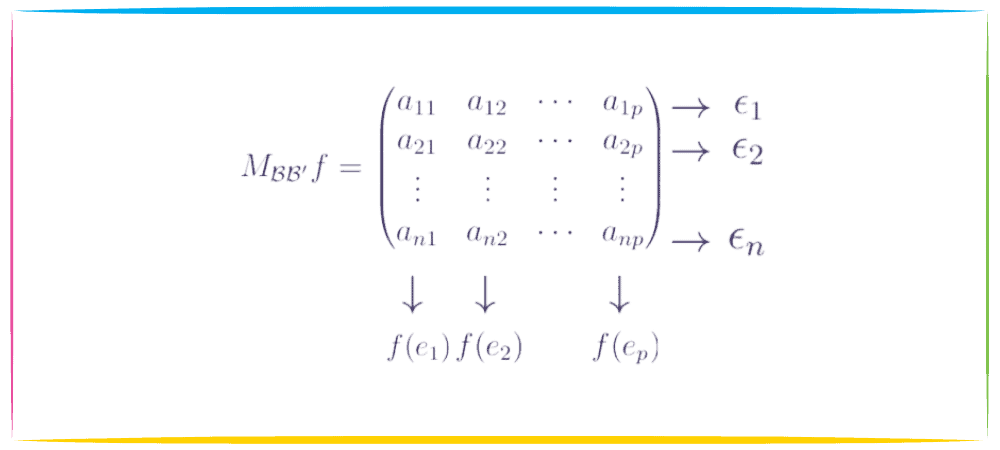
Et Hop ! Tu Obtiens Enfin Ta Fameuse Matrice
On remarque que pour un espace vectoriel de départ de dimension p et un espace vectoriel d’arrivée de dimension n, on obtient une matrice de taille n*p 👩🏫
Mais ne t’inquiète pas, le plus souvent tu rencontreras des endomorphismes et donc des matrices carrées 😁
4️⃣ Conclusion
Maintenant que tu as les outils et les connaissances pour maîtriser ces processus, les matrices d’applications linéaires ne sont plus un mystère pour toi !
Chaque étape, de la reconnaissance des vecteurs de base à l’assemblage des images dans la matrice, te rapproche d’une compréhension profonde de tes applications linéaires 🙌
N’oublie pas que la pratique est la clé !
Plus tu utiliseras ces techniques, plus tu seras à l’aise avec les concepts et capable de les appliquer efficacement lors de tes examens ou de tes concours 💡
Et toi, qu’en penses-tu ? Si tu as des questions ou si un point te semble flou, écris-moi en commentaire ! Je serai ravie de t’aider et de discuter avec toi. N’hésite pas non plus à partager ton avis ou tes propres astuces sur le sujet. Hâte de te lire ! 😊👇