Aujourd’hui, je te propose de plonger dans les secrets bien gardés de la famille Taylor
Non, il ne s’agit pas d’une nouvelle série Netflix, mais de quelque chose d’encore plus excitant (si, si, c’est possible) : les formules de Taylor !
Imagine une famille où chaque membre détient un pouvoir unique, capable de te révéler les mystères les plus profonds des fonctions mathématiques.
Les frères Taylor, sont prêts à te faire entrer dans leur monde, où prévoir le comportement d’une fonction devient un jeu d’enfant 👾
Tu te sens comme invité à une réunion de famille où chaque formule te révèle des secrets ancestraux sur les fonctions.
Et crois-moi, tu ne verras plus jamais les maths de la même manière !
Pourquoi Taylor est ton meilleur ami en maths ?
Imagine un instant pouvoir prédire l’avenir… Fascinant, n’est-ce pas ?
Eh bien, dans le monde magique des maths, les formules de Taylor te donnent ce super-pouvoir pour les fonctions !
Elles te permettent de savoir comment une fonction va se comporter autour d’un point, en te donnant une approximation aussi précise que tu le souhaites.
C’est un peu comme avoir une boule de cristal, mais pour les maths !
Alors, prêt(e) à faire connaissance avec les frères Taylor et à découvrir comment ils peuvent transformer ta vie académique ?
1️⃣ La formule de Taylor-Young
La première formule est comme la porte d’entrée dans le monde fascinant des approximations 🤩
Elle te dit que tu peux approximer n’importe quelle fonction (assez gentille pour se laisser faire) autour d’un point en utilisant sa valeur et ses dérivées en ce point !
Sympa, non ? C’est comme si tu pouvais prévoir le comportement de ta fonction avec juste quelques indices 😏
Mais attention ! On ne rentre pas comme ça dans le clan de Taylor-Young !
Il faut respecter une condition 🧐
Tu dois absolument être au moins n-fois dérivable sur ton intervalle de définition !
Si tu respectes cette condition alors Taylor-Young te donnera ton développement limité à l’ordre n au point que tu désires :
$$f(x)=f(a)+\sum_{k=1}^{n}\frac{f^{(k)}(a)}{k!}(x-a)^{k}+ o((x-a)^{n})$$
Le secret bien gardé ?
Tous les développements limités en zéro que tu utilises pour prévoir le comportement des fonctions au voisinage de zéro sont en fait un cas particuliers de Taylor-Young avec a=0 !
2️⃣ La formule de Taylor-Lagrange
La formule de Taylor avec le reste de Lagrange, c’est un peu l’assurance qualité de ton approximation 😎
Elle te dit précisément à quel point tu peux te tromper dans ton estimation !
C’est comme si, en plus de prévoir le futur, tu avais une marge d’erreur clairement définie 😌
Par contre, pour que Taylor-Lagrange te donne la formule pour prévoir ton futur, il faut respecter deux conditions :
- Être dérivable au moins n-fois sur [a;b]
- Être au moins (n+1)-dérivable sur ]a;b[
Alors seulement Taylor-Lagrange te donnera l’existence d’un réel c dans l’intervalle ]a;b[ tel que tu aies l’approximation suivante :
$$f(b)=f(a)+\sum_{k=1}^{n}\frac{f^{(k)}(a)}{k!}(b-a)^{k}+ \frac{f^{(n+1)}(c)}{(n+1)!}(b-a)^{n+1}$$
3️⃣ La formule de Taylor-Laplace
Et là, bam ! 💥
Juste quand tu pensais avoir tout vu, la formule de Taylor-Laplace, plus connue sous le nom de Taylor avec reste intégral, fait son entrée fracassante !
Taylor-Laplace te propose une aventure plus complexe et riche avec un « reste » sous forme d’intégrale qui te donne une précision hallucinante sur l’erreur d’approximation !
C’est comme si on te donnait une loupe magique qui révèle les moindres détails de ta fonction, te permettant de naviguer avec précision dans le vaste océan des maths 🌊
Cependant, avant de te révéler ses secrets, Taylor-Laplace te demande en échange d’être au moins de classe (n+1) sur l’intervalle [a;b] !
$$f(b)=f(a)+\sum_{k=1}^{n}\frac{f^{(k)}(a)}{k!}(b-a)^{k}+ \int_{a}^{b}\frac{(b-t)^{n}}{n!}f^{(n+1)}(t)dt$$
Le secret bien gardé ?
Il existe une autre écriture pour le reste intégrale de Taylor-Laplace qui en fonction de la situation peut s’avérer utile !
$$R_{n}(f)=\frac{(b-a)^{n+1}}{n!}\int_{0}^{1}(1-t)^{n}f^{(n+1)}(a+t(b-a))dt$$
💪 On fait un Petit Récap 💪
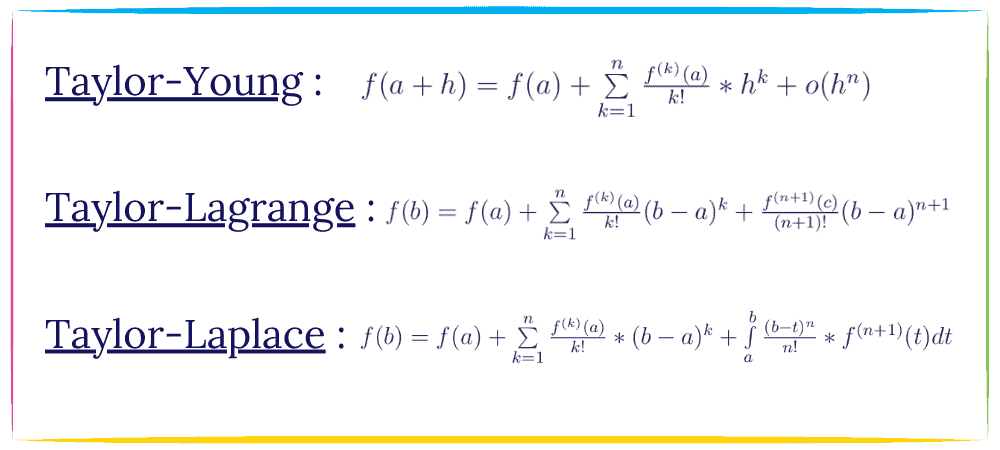
Prochain défi : appliquer Taylor dans ta vie
Je sais, je sais… Les maths peuvent parfois sembler être un monde obscur et intimidant 😣
Mais avec les formules de Taylor à ton arc, tu es désormais équipé(e) pour transformer ton stress en succès 😎
Chaque formule est une flèche qui te rapproche de la cible : comprendre et maîtriser les fonctions comme jamais auparavant !
Maintenant que tu connais ces formules magiques, pourquoi ne pas les appliquer ?
La prochaine fois que tu te retrouves devant une fonction complexe, sors ton arc de Taylor et vise juste 😉
Et toi, qu’en penses-tu ? Si tu as des questions ou si un point te semble flou, écris-moi en commentaire ! Je serai ravie de t’aider et de discuter avec toi. N’hésite pas non plus à partager ton avis ou tes propres astuces sur le sujet. Hâte de te lire ! 😊👇