T’es-tu déjà demandé si on pouvait représenter des rotations, des réflexions ou même des transformations dans l’espace, juste avec des matrices ?
Eh bien, la réponse est oui !
C’est là que les matrices orthogonales entrent en jeu !
Ces petites merveilles mathématiques permettent de traduire les mouvements géométriques en langage mathématique, tout en préservant les distances et les angles !
Et ce n’est pas tout ! Grâce aux matrices orthogonales, on peut résoudre des problèmes complexes en maths, en physique, ou même en informatique, tout ça en restant sur ta feuille de papier.
Imagine un film 3D : les rotations et les mouvements de caméra, c’est en grande partie grâce à elles ! Bluffant, non ?
Mais avant de se lancer dans la carrière d’un caméraman, on va plonger dans leur univers et découvrir comment elles fonctionnent, pourquoi elles sont aussi géniales, et surtout, comment les reconnaître en un clin d’œil
Tu vas voir, les matrices orthogonales n’auront plus de secrets pour toi !
Prêt·e ? C’est parti !
1️⃣ C'est quoi une matrice orthogonale ?
Commençons par le début, c’est-à-dire la définition ! Ça ne sera pas trop douloureux, promis
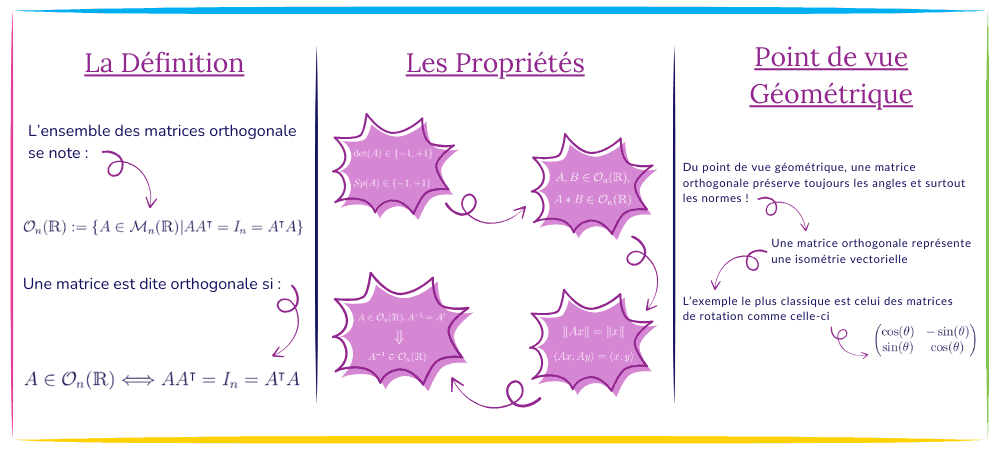
Définition : Une matrice \(A\in\mathcal{M}_n(\mathbb{R})\) est dite orthogonale, si elle vérifie l’égalité suivante $$AA^T= I_n=A^T A$$
Où \(I_n\) est la matrice identité
Remarque : en pratique on ne montre qu’un côté de cette égalité : \( AA^T= I_n\) ou \( A^T A=I_n\)
Ce n’est pas tout ! Comme toute nouvelle famille d’objet en mathématiques, on lui associe un nouvel ensemble avec une nouvelle notation à connaître !
Toujours plus de notation à savoir, on adore ça
L’ensemble des matrices orthogonales est noté \(\mathcal{O}_n(\mathbb{R})\)
Petite Remarque : la même définition est bien entendu valable pour les matrice de \(\mathcal{M}_n(\mathbb{C})\), cependant comme les trois quarts du temps on est dans les réels je vais restreindre les définitions et propriétés de cet article dans \(\mathbb{R}\). Garde bien à l’esprit que tout restera juste dans \(\mathbb{C}\)
Propriété : Toute matrice orthogonale est bien entendu inversible, et son inverse est tout simplement sa transposée \(A^T\) !
Tu te rends compte ! Au lieu de passer des longues minutes à faire la méthode miroir pour inverser tes matrices 3*3, 4*4 ou pire encore 
2️⃣ Les petites propriétés des matrices orthogonales
Les matrices orthogonales ne sont pas juste stylées, elles ont aussi plein de propriétés utiles !
Commençons par des petites propriétés directes
Propriétés : Soit \(A,B\in\mathcal{O}_n(\mathbb{R})\), alors :
- \(A^{-1}=A^T \) et \(A^{-1}\in\mathcal{O}_n(\mathbb{R})\)
- \(A*B\in\mathcal{O}_n(\mathbb{R})\)
Continuions notre découverte du monde des matrices orthogonales avec le lien entre orthogonalité et valeurs propres
Propriétés : Soit \(A\in\mathcal{O}_n(\mathbb{R})\), alors :
- \(\det(A)\in \{-1, +1\}\)
- \(Sp(A)\in \{-1, +1\}\)
N’est-ce pas génial ça ! Pas besoin de t’embêter à calculer le polynôme caractéristique pour les matrices orthogonales, tu connais déjà leurs valeurs propres
Et pour finir, rien de mieux que deux petites propriétés qui vont introduire la partie suivante de cet article !
Propriétés : Soit \(A\in\mathcal{O}_n(\mathbb{R})\), alors :
- \(\forall x\in\mathbb{R}^n, \left\| Ax \right\|=\left\| x \right\|\)
- \(\forall x,y\in\mathbb{R}^n, \langle Ax,Ay \rangle=\langle x,y \rangle\)
4️⃣ Le point de vue géométrique
La dernière propriété qu’on a vu est très importante du point de vue géométrique !
Dire que \( \forall x\in\mathbb{R}^n, \left\| Ax \right\|=\left\| x \right\| \) revient à dire qu’en fait les matrices orthogonales préservent les normes 😎
Ce petit détail est tellement essentiel en géométrie, qu’on lui a même donné un nom : isométrie vectorielle !
Définition : Une isométrie vectorielle est une application linéaire qui conserve les distances
En gros, les matrices orthogonales représentent les isométries vectorielles d’un point de vue matriciel 🙌
Les isométries ou matrices orthogonales ne conservent pas que les distances 😏 On a pu voir que les matrices orthogonales conservent aussi le produit scalaire, mais pas que !
Propriété : Les matrices orthogonales préservent les angles
D’ailleurs, il existe plusieurs types d’isométrie vectorielle que ce soit en dimension 2 ou 3
On y retrouve par exemple les symétries axiales, les translations, les symétries glissées, les vissages, etc..
Mais l’exemple le plus classique et que tu rencontres tout le temps, c’est les rotations 🙃
Par exemple, en dimension 2, la matrice d’une rotation va ressembler à ça 👇
$$\begin{pmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta) \\
\end{pmatrix}$$
5️⃣ Comment les reconnaître facilement ?
Maintenant, qu’on a vu à quel point ses matrices étaient géniales, tu te demandes sûrement comment les identifier rapidement ? 🕵️♀️
Je vais te donner quelques caractérisations qui te permettront de savoir ultra rapidement si ta matrice est orthogonale ou non !
- \(A\in\mathcal{O}_n(\mathbb{R})\Longleftrightarrow AA^T= I_n=A^T A\)
- \(A\in\mathcal{O}_n(\mathbb{R})\Longleftrightarrow \text{ ses colonnes forment une base orthonormée de } \mathbb{R}^n\)
- \(A\in\mathcal{O}_n(\mathbb{R})\Longleftrightarrow \text{ ses lignes forment une base orthonormée de } \mathbb{R}^n\)
💪 On fait un Petit Récap 💪
Et toi, tu connaissais déjà tout ça ? 🤔
💬 Dis-moi en commentaire :
- Est-ce que tu as déjà rencontré des matrices orthogonales dans tes exos ?
- Si oui, c’était clair comme de l’eau de roche ou tu as dû t’accrocher pour les comprendre ?
- Et surtout, as-tu déjà eu l’occasion de les utiliser dans un domaine concret, comme la physique, l’informatique, ou même en modélisation 3D ?
👉 N’oublie pas de partager cet article avec tes potes qui galèrent en maths. Ils te remercieront, promis ! 🤝