Tu pensais qu’il n’existait qu’une seule moyenne en maths ? Erreur de débutant 😏
Si je te dis moyenne, tu penses direct à la moyenne arithmétique… et puis c’est tout, après tout tu en as appris qu’une seule !
Pourtant, il en existe plusieurs, et chacune a son utilité bien précise 🙌
Dans cet article, je t’explique les 4 moyennes que tu dois absolument connaître si tu fais des statistiques !
Allez, c’est parti ! 🚀
1️⃣ Le moyenne arithmétique
C’est celle que tu connais déjà, celle que tu as appris dès le collège !
👉 Tu l’utilises pour faire pratiquement la moyenne de n’importe quoi, comme par exemple la moyenne de tes notes
📌 Formule : $$\bar{x}=\frac{\sum\limits_{i=1}^k x_i}{\sum\limits_{i=1}^k n_i}$$
🧠 À Retenir : c’est LA base. Elle fonctionne super bien quand toutes les données ont le même poids dans ta série statistique !
2️⃣ La moyenne géométrique
Tu l’as peut-être croisée sans la remarquer…
Pourtant elle est hyper puissante quand les données varient de manière multiplicative, comme par exemple des taux de croissance 📈
📌 Formule : $$G=\big( \prod\limits_{i=1}^k x_i^{n_i}\big)^{\frac{1}{\sum\limits_{i=1}^k n_i}}$$
💡 Exemple : si tu analyses des rendements d’investissement ou des pourcentages de progression d’une population, c’est elle qu’il te faut !
3️⃣ La moyenne harmonique
C’est la moyenne spéciale vitesse et déplacements 🏃♂️
Tu bosses sur un exo où on te parle de deux trajets à des vitesses différentes ? Ne sors surtout pas ta moyenne arithmétique !
👉 Ici, c’est la moyenne harmonique qui fait le taf !
📌 Formule : $$H=\frac{n}{\sum\limits_{i=1}^k n_i\frac{1}{x_i}}$$
🧠 Elle est parfaite pour les situations où le temps est fixe, mais les vitesses changent !
4️⃣ La moyenne quadratique
Elle va te donner du poids au grandes valeurs 💪
Si tu veux donner plus d’importance aux grandes valeurs dans ton calcul ? Alors la moyenne quadratique (aussi appelée RMS pour les intimes) est ton alliée 😎
📌 Formule : $$Q=\sqrt{\frac{\sum\limits_{i=1}^k n_ix_i^2}{\sum\limits_{i=1}^k n_i}}$$
💡 Elle est souvent utilisée en physique (pour des courants électriques par exemple ⚡) mais aussi en traitement de données !
💪 On fait un Petit Récap 💪
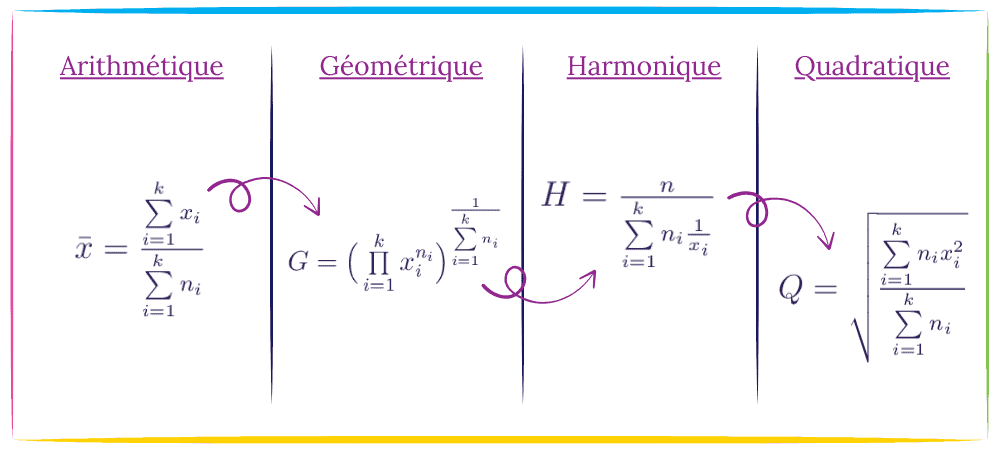
En résumé, il n’y a pas que la moyenne arithmétique en statistiques !
Même si c’est souvent elle qu’on va utiliser, en fonction de certains cas dans lequel on va se trouver les autres moyennes seront beaucoup plus adaptées !
D’ailleurs, il en existe encore d’autres des moyennes, comme par exemple la moyenne mobile qui, elle, va te permettre de lisser les fluctuations statistiques par exemple 😉
Et toi, t’en connaissais combien sur les 4 ? 🙋♀️
Dis-le-moi en commentaire ⬇️
À très vite pour un nouvel article qui rend les maths (presque) fun 💜